
الصيغة الأسية للعدد المركب 2 Http Ift Tt 2dsoznp الأرقام المركبة للدورة توضح الأرقام المركبة الأرقام المركبة للدورة التدريبية الأرقام المركبة المنهج البحث عن الكلمات لغز الكلمات المدونة
ملخص الارقام المركبة اكاديمية البكالوريا بالجزائر فيس بوك

قيم مبررة لـ Cos و Sin في الأعداد المركبة على Youtube

عمدة رقم مركب ويكيبيديا
الأعداد المركبة طبيعة المثلث باك بور توت لوموند فيس بوك

جدول شطب 2021 الصف الثاني متوسط لجميع المواد رسمياً من الوزارة صور واضحة جداً وجاهزة للطباعة. أهلا وسهلا بكم متابعين موقع وقناة السيد أحمد مهدي شل. في 2021 الجدول الدوري

مضاعفة الأعداد المركبة وخصائص عملية الضرب شرح مفصل لعملية ضرب الرقم.
الخصائص المركبة. في هذا البرنامج التعليمي ، سوف نتعلم كيفية استخدام خصائص الأرقام المرتبطة بالأرقام المركبة للعثور على قيمة التعبير. 7- استخدام دستور Mowafer لحل مسائل الأعداد المركبة في. في هذا الدرس ، سوف نتعلم كيفية استخدام خصائص الأعداد المترافقة للأعداد المركبة لإيجاد قيمة التعبير.
في هذا المقال نقدم لك شرحًا وبحثًا عن خصائص الأعداد الحقيقية بالأمثلة الموضحة. يمكن تعريف الأرقام على أنها مجموعة من الرموز التي تستخدم للتعبير عن الأرقام التي تقع بين صفر وتسعة ، وبالتالي فهي لا تعتبر أرقامًا ، بل بالأحرى. الرياضيات – حل المعادلات في الأعداد المركبة – حل المعادلة التربيعية في مجموعة من الأعداد المركبة. 3 بعض خواص العمليات المركبة الأعداد المركبة تشبه الأعداد الحقيقية وتختلف عنها في نواح كثيرة. فيما يلي سنقوم بإدراج بعض خصائص الأعداد المركبة على النحو التالي: 1 يساوي عددين مركبين.
ملخص الأعداد المركبة في الرياضيات للسنة الثالثة الثانوية التقسيمات العلمية. أقدم لكم الخصائص والعلاقات في درس الأعداد المركبة مع شرح قسم العلوم التجريبية. أحد المفاهيم المهمة المتعلقة بالأعداد المركبة هو اتحادات الأعداد المركبة.
إنها الأرقام التي يمكن كتابتها بالصيغة التالية AABC حيث أن B تمثل الأعداد الحقيقية و T تساوي جذر -1. يسمى A الجزء الحقيقي من العدد المركب ، بينما B هو الجزء. خواص الأعداد المركبة أي من العبارات التالية ينطبق على رقمين مركبين متساويين أ أجزائهما الحقيقية ستكون متساوية وأجزاءهما التخيلية غير متساوية. في التعبيرات التي تتضمن ضرب وقسمة العديد من الأعداد المركبة ، من المفيد البحث عن عوامل مشتركة أو إذا كان بإمكاننا تطبيق بعض خصائص الأعداد المركبة لتبسيط العمليات الحسابية.
الفكرة هي توسيع الأعداد الحقيقية في الوحدات التخيلية i حيث i 2 1 displaystyle i2-1 والتي تمكننا من إيجاد حل للمعادلة أعلاه. توفر الأعداد المركبة حلاً لهذه المعضلة. 5- التعبير عن خصائص الأشكال الهندسية باستخدام الأعداد المركبة. 6- توظيف خواص long و omda لحل مسائل الأعداد المركبة في الهندسة.
خصائص الأرقام المركبة وموسيقى دندنها وأغاني mp3. نتج عن نظام الأعداد المركبة أو تم اختراعه كنتيجة مباشرة لحل المعادلة Q2 1 0 حيث Q2-1 وعن طريق أخذ الجذر التربيعي لكلا الجانبين وجدنا أن الجذر التربيعي الذي يقع تحته الرقم -1 وهذا يعني أن هناك عددًا تم ضربه في نفسه مما يعطينا -1 وهذا. 08 أبريل 2020 الجلسة 02 في الأعداد المركبة.

دبوس في الصف العاشر ملفاتي الإماراتية

الجدول الدوري الحديث والتدرج في خصائص العناصر ، الصف العاشر ، الكيمياء ، Borobenet ، ملصقات فيلم الخط العربي

أرقام الكم كيمياء الكم

دائرة مثلثية وأرقام مركبة يوتيوب

مثال 5 جمع وطرح الأعداد المركبة يوتيوب
الأعداد المركبة طبيعة المثلث باك بور توت لوموند فيس بوك

ملخص الارقام المركبة موقع السيد قويس فاتح
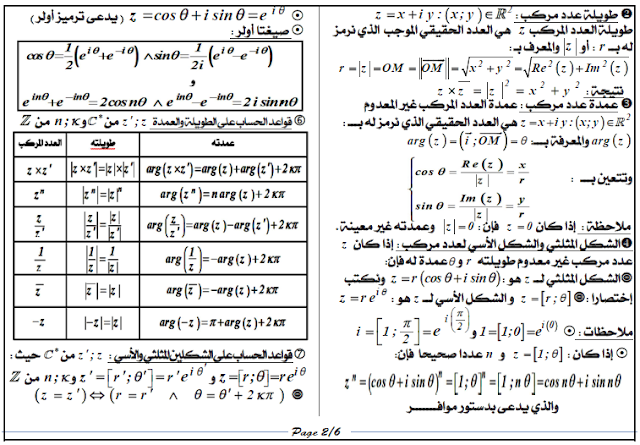
ملخص كامل ومفصل للأعداد المركبة لطلاب البكالوريا الرياضية المبرمجة
الأعداد المركبة طبيعة المثلث باك بور توت لوموند فيس بوك

الأعداد المركبة والأمثلة من حولهم


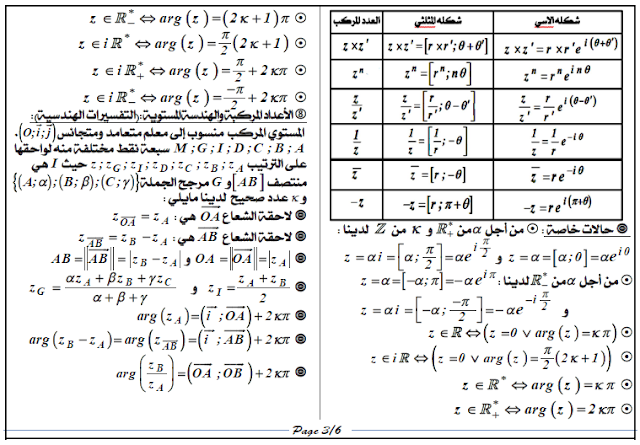
ملخص كامل ومفصل للأعداد المركبة لطلاب البكالوريا الرياضية المبرمجة
الأعداد المركبة طبيعة المثلث باك بور توت لوموند فيس بوك





